Le problème
Julie a travaillé sur un très joli problème de mathématiques.
Comment l'auriez-vous résolu ? Selon vous, y'a-t-il une autre méthode que le 'tâtonnement' ? Y'a-t-il plusieurs solutions ?
Lorsque j'ai vu ce devoir, j'ai immédiatement identifié une variante (simple) du Knapsack (= problème du sac à dos) !
Il s'agit de :
- maximiser le chargement du camion,
- respecter la contrainte des 200 Kg.
La complexité du problème augmente considérablement si :
- on augmente le choix de caisses (poids différents, nombre)
- on ajoute une contrainte de volume (volume max du camion, volume des caisses).
Trouver une solution idéale
Qui trouvera la solution consistant en un chargement optimisé en poids et en respectant le volume disponible ?
Rien de tel qu'un petit tour dans Excel (et son extension 'Solver') pour proposer une ébauche de solution, en tous cas pour le premier voyage du camion.
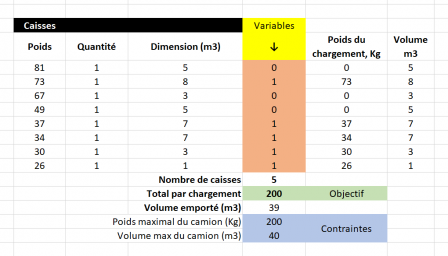
La construction de mon tableau Excel consiste en :
- une liste des caisses à disposition (types et quantités)
- la multiplication du nombre de caisses par leur poids et volume
- lister les contraintes (poids max du camion, volume max)
- une colonne des variables (la quantité des caisses à prendre)
- une cellule de l'objectif à atteindre.
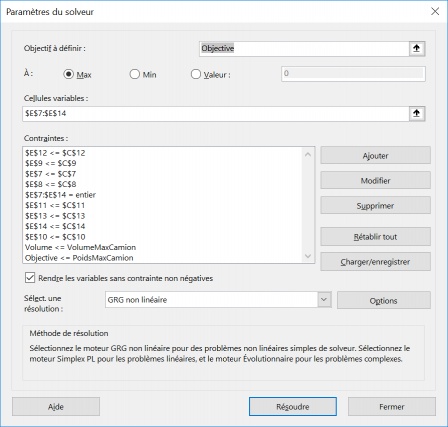
Le Solveur
Excel et son solveur sera donc en charge de maximiser le poids du chargement en jouant avec la quantité des caisses (variables), tout en respectant les contraintes imposées.
Des contraintes ont été ajoutées, notamment celle indiquant que le nombre de caisses doit être entier. Ou celles qui évitent au Solver d'embarquer davantage de caisses que celles à disposition.
Pour en savoir plus: Wikipedia donnera des informations intéressantes sur le Knapsack Problem ou la même page, en français.
Le site Microsoft détaille l'utilisation du Solver.

1 De Koobor -
Si le total des caisse fait à peu près 400KG, on en déduit que le poids moyen est d'env. 50KG.
Il faut assembler 2 caisses dont le poids total se rapproche le plus possible de 100KG, ces 2 caisses doivent voyager ensemble.
On peut faire une opération supplémentaire en calculant la différence entre le poids de la caisse et la moyenne de 50KG, les résultats montrent plus clairement quelles sont les caisses qui vont ensemble :
81 -> +31
73 -> +23
67 -> +17
49 -> -1
37 -> -13
34 -> -16
30 -> -20
26 -> -24
On a donc +23 et -24 (-1) et +17 et -16 (+1)
Ce qui donne le premier convoi.
Les autres caisses vont dans le second convoi.
Mais j'ai l'impression que c'est une approche logique avec un peu de tâtonnement.